One thing that really annoyed me at the beginning of my adventure with Prolog was when THIS happened:

?- between(1,3,A).
A = 1 █ <- blinking cursor

I couldn't understand Why Prolog wouldn't produce all the solutions? It felt so obvious, that A can have 3 different results.

When working with predicates (fancy name for function as far as I am concerned), they not only produce value as in the other programming languages. They can produce something along the lines of "hey, here's a result, but you know, I have more, so get back to me if you want, m'kay?".

This "I have more" is called a Choicepoint.

At the end of this article I'll put excerpt from documentation which mentions how different types of predicates are making those, but it's not very relevant right now.

For above query, that is:

between(1,3,A).

Prolog might construct something that looks like a tree with 2 choicepoints:

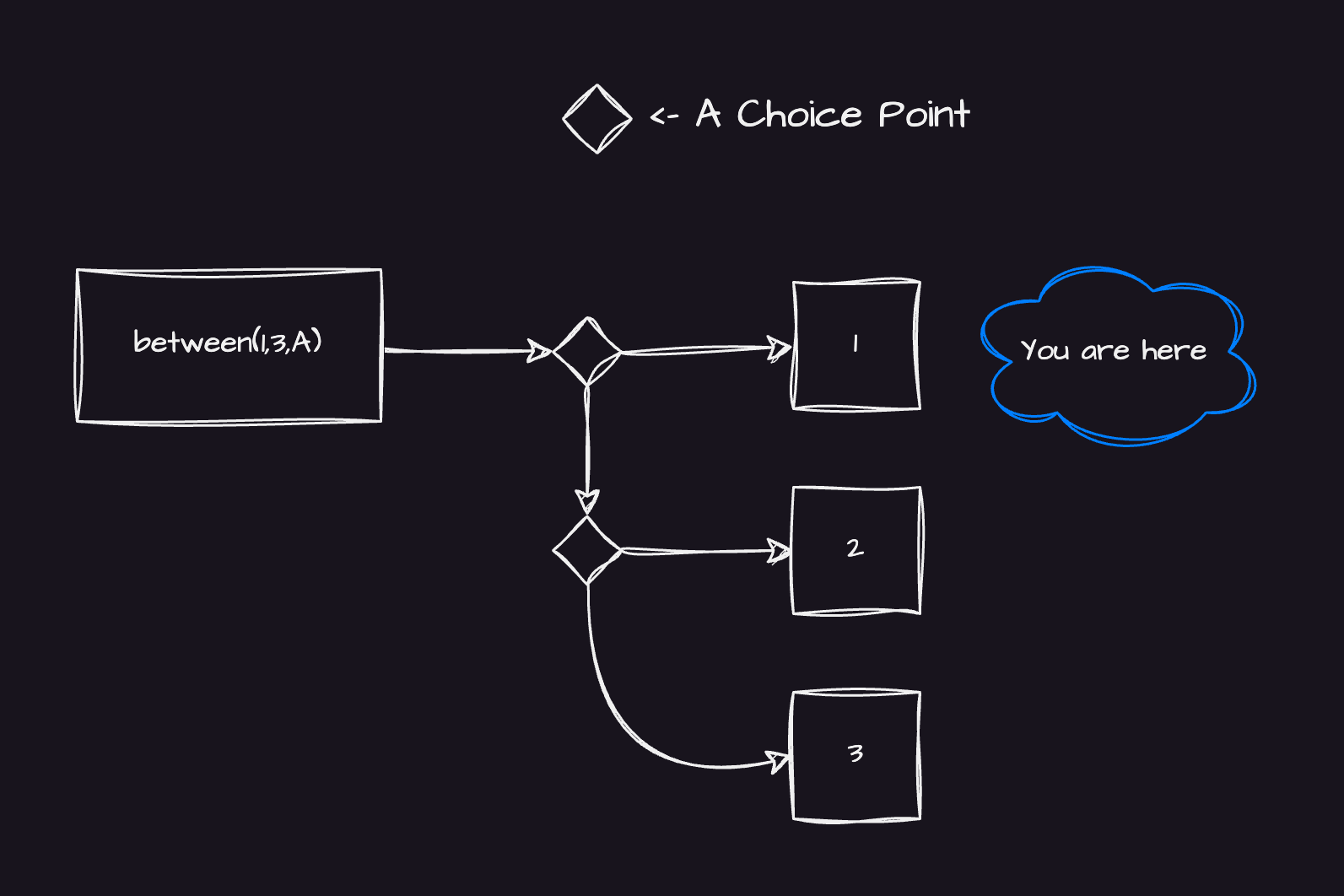
Note, that you never actually STOP at the choice point. Prolog needs to know about it, and you just moves through it. What you're exploring by query is a one of the final realities (or branches).

Because of that, Your (as a Query Maker), journey looks like this:

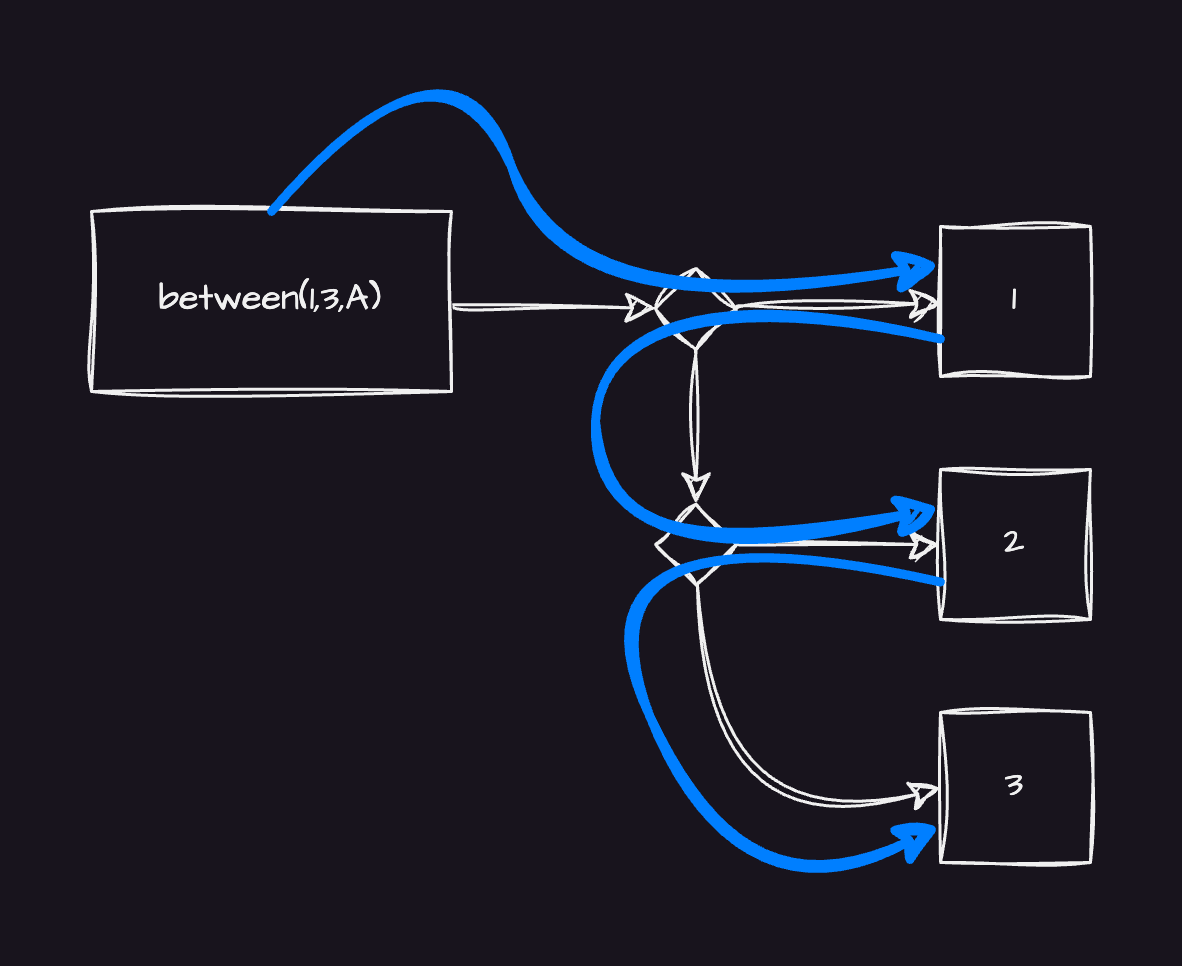
There's important term I feel should be: backtracking.

When you're at the end of the path and there are Choicepoints to navigate, asking Prolog to move back is called a backtracking. Familiarity with it is rather important because it often is mentioned in documentation.

I like to joke that writing Prolog is like building a forest: planting trees, mixing and prunning. Creation of Forest of Possibilties, and then exploring it. Another strong point for Prolog - it's not only logical and pragmatic, but also romantic! Who would've known!?

But, back to our solution trees, though. Let's consider more complex example:

List = [A,B], between(1,3,A), member(B, [cat,dog,fish]).

It's quite visible that we can produce 9 possible results which Prolog will happily spoon feed to us. (and by the way ; is a way in CLI to tell it "give me more!", while a simple . means "enough already!")

Visualized, it might look like this:

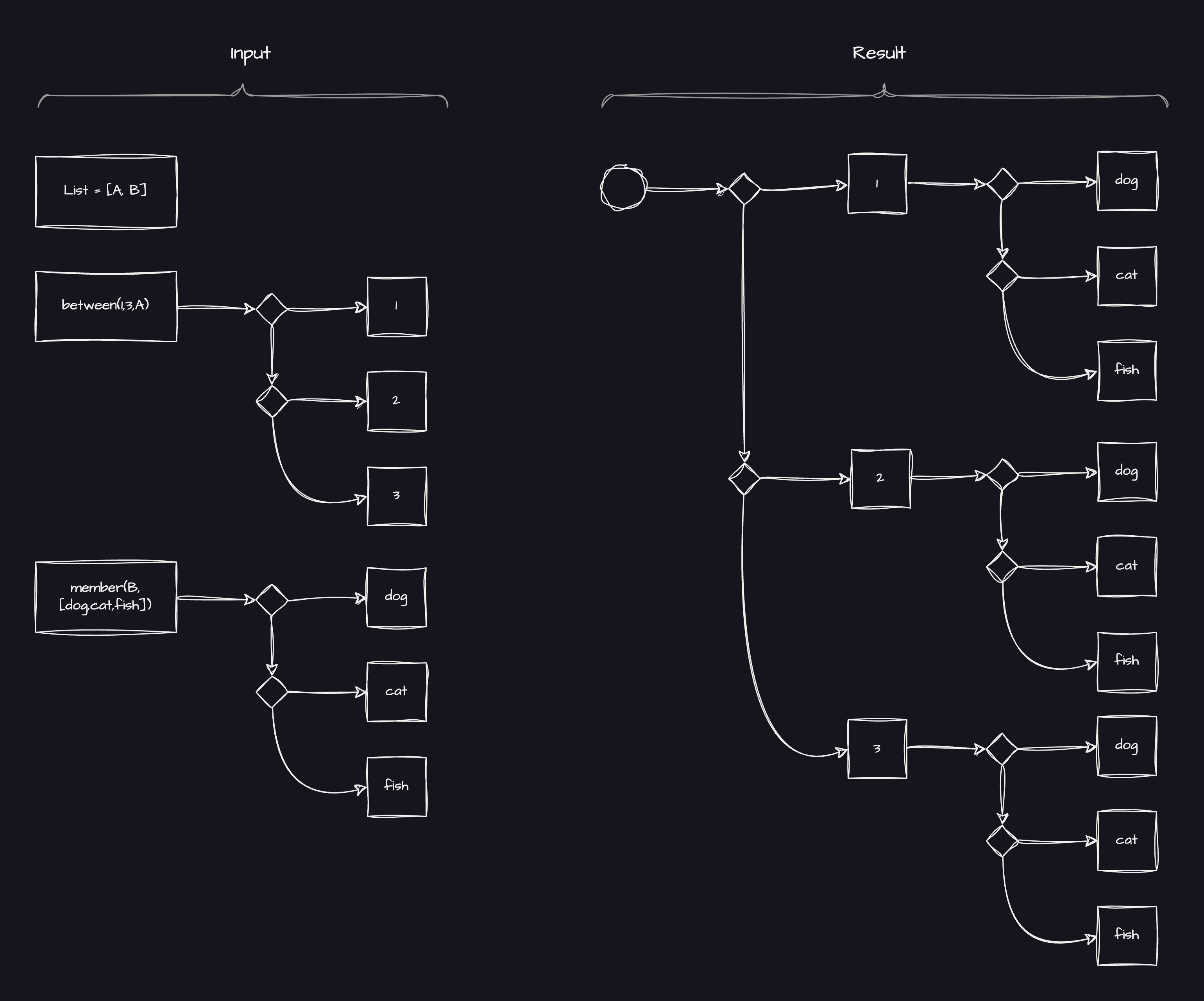
Whoa. Big one.

Even with only two basic clauses the tree gets rather big and unwieldy for presentation.

What would be the journey here? I suppose you know already, but let's use the diagram I already drew before writing this words, and I'm not sure where to put it.

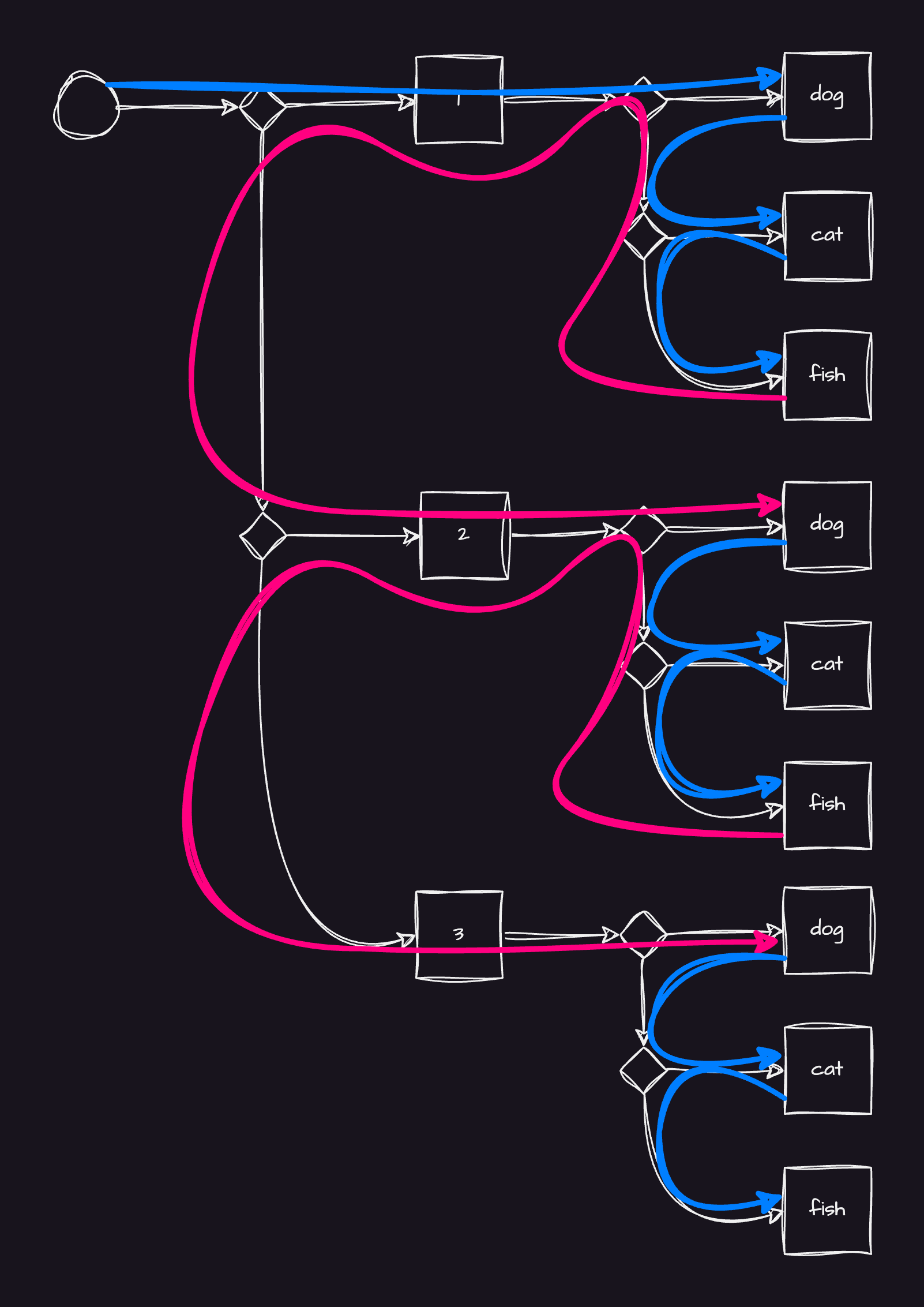
Two different colors is only to help show longer backtrack vs short one. They are completely the same.

And that's it! You know about choicepoints AND backtracking, which means that you have almost everything you need to start building your own Forest of Possibilities.

Few random notes:

• Prolog is not guessing from facts you wrote - it is following completely predictable path
• Changing the order of clauses will result in different tree, which might be important
• It's possible (with some advanc-ish operators) to shape Prolog's journey, i.e. same result can be either boring stroll across billion of possibilities or a Theseus-like *​cut* through Maze of the Infinite.

Extra: Predicate Types

As I mentioned before, it's easy to figure out whether choicepoint will be created or not, but it's not essential.

But sometimes it's good to know how we can confirm our hunch or clear doubt when unfamiliar semidet doesn't create a choicepoint.

Those are taken directly from SWI-Prolog Predicate Documentation, but - to save you some bandwidth and my personal repetition: there might be following types of predicates:

• det - 1..1 Results. No Choicepoints. E.g. flatten(List, Flattened) - it always succeeds and only one version exists
• semidet - 0..1 Results. No Choicepoints. E.g. max_member(Max, List) - if list is empty, it will fail, otherwise return same max result.
• nondet - 0..N Results. Undefined Choicepoints. Some may even leave Choicepoint AFTER last solution. subseq(List, Subseq, Rest) is nondet. Below an example of both behaviors, but in short sometimes predicate might be like "I don't know how long our journey will last"
• multi - 1..N Results. Undefined Choicepoints as above.

Finally there's also undefined but it's well..

nondet might also be confusing, so an example based on subseq:

% I asked for subsequence with 1 less element.
% There is choicepoint after last one,
% Prolog has no way of knowing if it read all.
?- subseq([1,2], A, [_Any]).
A = [2],
_Any = 1 ;
A = [1],
_Any = 2 ;
false.

% I asked for subsequence with any tail.
% When subseq reaches identity solution
% (i.e. [1] is subsequence of [1]), it knows
% there can't be more and leaves no choicepoint.
?- subseq([1], A, _Any).
A = [],
_Any = [1] ;
A = [1],
_Any = [].